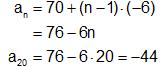Aritmeettisen lukujonon yleinen ja 20. termi
Kysymys 1 / 2
Muodosta seuraavien aritmeettisten lukujonojen yleinen eli n. termi ja laske jonon 20. termi.
Käytä apuna aritmeettisen lukujonon kaavaa

Muodosta aritmeettisen lukujonon yleinen ja 20. termi, kun..
1.
Aritmeettinen ja geometrinen lukujono ja summat
Käytä apuna aritmeettisen lukujonon kaavaa

Muodosta aritmeettisen lukujonon yleinen ja 20. termi, kun..
1.

Aritmeettinen ja geometrinen lukujono ja summat
Question Popup:
Lukujonoa kutsutaan aritmeettiseksi, jos jonon seuraava termi saadaan lisäämällä edelliseen (tai vähentämällä edellisestä) aina tietty sama luku. Tätä lukua kutsutaan erotusluvuksi
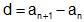
Esimerkiksi aritmeettisen lukujonon 1, 4, 7, 10, ... erotusluku on 3.
Lukujonoa kutsutaan geometriseksi, jos jonon seuraava termi saadaan kertomalla (tai jakamalla) edellinen termi aina tietyllä samalla luvulla. Tätä lukua kutsutaan suhdeluvuksi
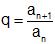
Geometrisen lukujonon -1, 2, -4, 8, -16, ... suhdeluku on -2.
Aritmeettisen ja geometrisen lukujonon yleisille termeille on omat kaavansa. Lukujonojen peräkkäisten jäsenten summat taas saadaan laskettua aritmeettisen ja geometrisen summan kaavan avulla. Kyseiset kaavat löytyvät taulukkokirjasta.

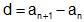
Esimerkiksi aritmeettisen lukujonon 1, 4, 7, 10, ... erotusluku on 3.
Lukujonoa kutsutaan geometriseksi, jos jonon seuraava termi saadaan kertomalla (tai jakamalla) edellinen termi aina tietyllä samalla luvulla. Tätä lukua kutsutaan suhdeluvuksi
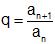
Geometrisen lukujonon -1, 2, -4, 8, -16, ... suhdeluku on -2.
Aritmeettisen ja geometrisen lukujonon yleisille termeille on omat kaavansa. Lukujonojen peräkkäisten jäsenten summat taas saadaan laskettua aritmeettisen ja geometrisen summan kaavan avulla. Kyseiset kaavat löytyvät taulukkokirjasta.

Solution Popup:
Aritmeettisen lukujonon yleinen termi saadaan kaavasta
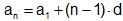
Sijoitetaan kaavaan annetut arvot ja muodostetaan yleisen termin ja 20. termin lausekkeet.
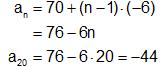
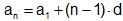
Sijoitetaan kaavaan annetut arvot ja muodostetaan yleisen termin ja 20. termin lausekkeet.