Normaalijakauma: laskuesimerkki
Kysymys 1 / 3
Ratkaise tehtävä.
Oletetaan, että x noudattaa normitettua normaalijakaumaa. Laske todennäköisyys, että x saa arvon, joka on pienempi kuin 2.
Oletetaan, että x noudattaa normitettua normaalijakaumaa. Laske todennäköisyys, että x saa arvon, joka on pienempi kuin 2.
Question Popup:
Normaalijakaumaa koskevia laskuja suoritetaan seuraavalla tavalla taulukkokirjan avulla. Tutkitaan normitettua normaalijakaumaa, sen keskiarvo on siis 0 ja keskihajonta 1. Taulukkoon on merkitty todennäköisyyksien arvoja sille, että saadaan muuttujan arvoa pienempi arvo, sitä kuvataan seuraavasti:
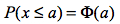
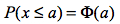
Funktiota kuvaava merkki on kreikankielen aakkonen fii ja funktion arvo voidaan lukea suoraan taulukkokirjasta. Normaalijakaumassa todennäköisyys, että päädyttäisiin yhteen tiettyyn arvoon ajatellaan nollaksi. Näin ollen ei ole merkitystä onko muuttuja pienempi vai pienempi tai yhtäsuuri.
Solution Popup:
Likiarvo saadaan esimerkiksi taulukkokirjasta. Yleensä tämä normaalijakauman kertymäfunktio kuvataan taulukkona, jossa vasemmasta pystysarakkeesta luetaan kysyttävän luvun ykköset ja kymmenesosat ja ensimmäiseltä vaakariviltä valitaan sen sadasosat. Nyt etsitään siis kohdat 2,0 ja 0 ja näiden risteyskohdasta löytyy luku numerosarja 9772, joka tulkitaan desimaaliluvuksi 0,9772.
Kyseinen funktio ilmoittaa siis sen todennäköisyyden, että arvo osuu jonnekin normaalijakauman osoittamalla pinta-alalle ennen kohtaa a.